This tutorial shows how to assemble Worm Gears (that are imported) in SpaceClaim. These are typically used for very high reduction of speed in shafts (hence very high gain in torque) when the space is limited. The axes of shafts are skew and the angle between them is usually 90 degrees.
Update (July 20, 2012): Considered number of starts/threads in the worm in the equations.
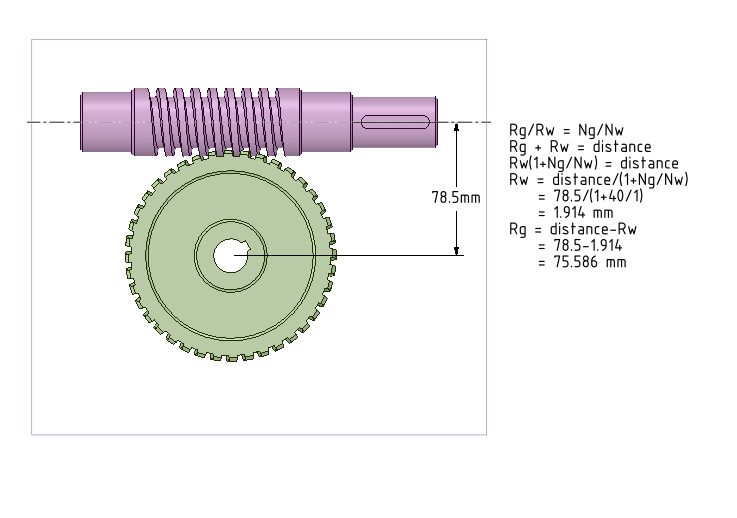
When a worm gear assembly is imported inside SpaceClaim, we need to define Gear Condition/Constraint between them, which is done by selecting two cylindrical surfaces. The main task is to find out the radii of these mating cylinders (also known as Pitch Radius). The following diagram shows the equations of determining the radii Rg (Radius of gear) and Rw (Radius of worm) of the two cylinders, given the number of teeth in the gear(Ng), number of threads/starts in the worm (Nw) and the distance between the axes of the gears. We have two equations with Rg and Rw and solving for Rg and Rw is simple.
In the video tutorial below:
- We have imported a Worm Gear Assembly from GrabCAD.
- The revolute joints (consisting of a Align condition + Tangent condition) are defined so that worm and gear have a freedom to rotate (degree-of-freedom) about their axes.
- The pitch cylinders are determined in the form of surfaces (which do not add up to the mass of the components)
- Gear condition is defined between them.
- Worm is rotated and the gear rotates due to meshing.
- Go to SC-Motion. Gear conditions are made use of in the solver and simulation is done.
The SpaceClaim assembly file (with Gear condition defined) can be downloaded here.
The video tutorial can be downloaded here
We have similar tutorials for External Gears, Internal Gears, Rack and Pinion and Bevel Gears.